The Circle: The Shape with the Largest Area Among Equal Perimeters
Written on
The Significance of Circular Tables
In my childhood home, we always had a round dining table. I recall hearing from the elders that this shape accommodated more people than a rectangular one. At the time, I wasn't sure if this was true, though it seemed reasonable.
Throughout my visits to various restaurants, especially those with Asian influences, I've noticed that the largest tables tend to be round. Could this be due to a round table providing extra space for dishes during large gatherings?
Jakob Steiner, a Swiss mathematician from the 1800s, pondered this question. This article aims to elucidate his proof that among all closed curves in a plane with equal perimeters, the circle encompasses the largest area.
Understanding Shapes and Their Areas
Consider a string measuring 1 unit in length. The simplest closed shape we can create with this string is a triangle (3 sides), followed by a rectangle or square (4 sides). Which of these shapes has a larger area?
To simplify, let’s compare an equilateral triangle to a square. The area of an equilateral triangle can be calculated using the “Side-Angle-Side” formula:
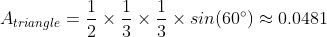
Meanwhile, the area of a square is determined as follows:
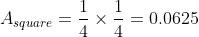
From this comparison, we can conclude that for shapes with the same perimeter, a square has a larger area than an equilateral triangle. Now, how does a regular hexagon fare in this comparison? A regular hexagon can be visualized as being formed by six equilateral triangles, each with a side length of 1/6. Its area can be calculated as follows:
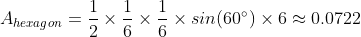
It appears that as we examine closed shapes with the same perimeter, the area increases with the number of sides. The shape with the most sides possible is a circle. The area of a circle with a perimeter of 1 can be expressed as:
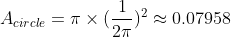
Based on these explorations, the initial hypothesis seems to hold true.
Jakob Steiner's Contributions
Between 1830 and 1840, Jakob Steiner sought to validate the hypothesis by demonstrating that the following three principles apply to the areas of closed shapes with identical perimeters:
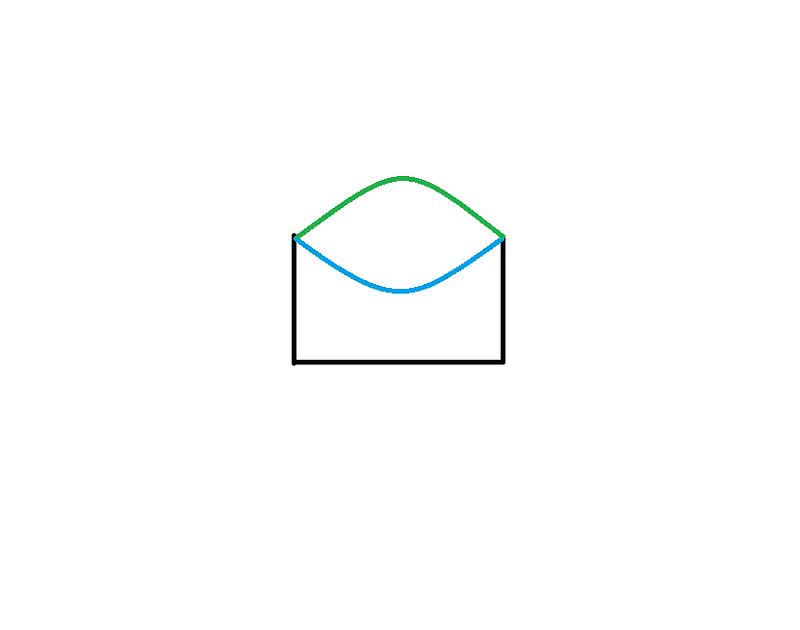
- Concavity and Area: Closed shapes that have a greater area cannot be concave. This becomes evident when visualizing a four-sided shape. If two shapes have sides of equal length but differ in concavity, the one that bulges outward (green line) has a larger area than the inward-bulging shape (blue line), despite having the same perimeter.
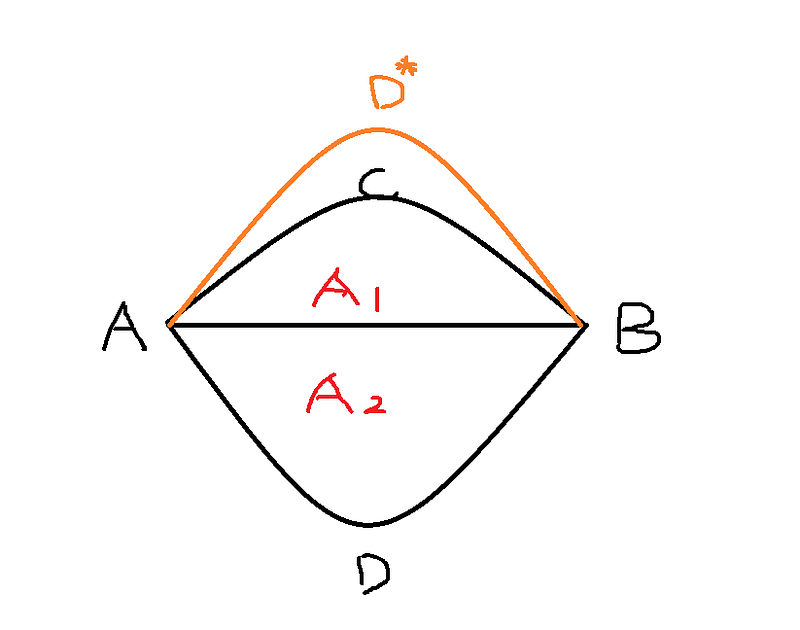
- Equal Division of Perimeter and Area: A line that divides the perimeter of a shape into two equal lengths does not necessarily divide the area equally. In the diagram below, line AB divides the perimeter of shape ACBD equally, but the areas on either side are not equal.
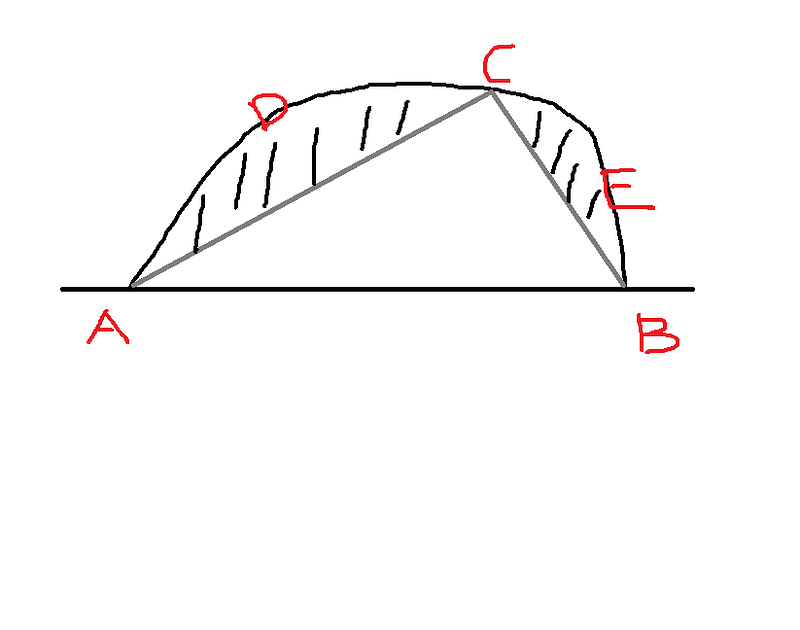
- Semi-Circles and Area Maximization: Among all closed shapes connecting three points on a plane, a semi-circle has the maximum area. By considering different shapes connecting points A, B, and C, we can deduce that the area is maximized when angle ACB is 90 degrees, confirming that the semi-circle offers the largest area.
Further Insights
While these three principles seem to support the hypothesis, scholars have pointed out that Steiner's proof assumed the existence of a solution, an aspect he did not explicitly address. Nevertheless, I believe these principles are fascinating from a geometric standpoint, and I wanted to present them in a more accessible manner.
The property of the circle was ultimately established by another mathematician through the calculus of variations, a topic I encourage readers to explore further.
Understanding why the circle encloses the largest area among shapes with the same perimeter can be illustrated effectively through visual examples. The video titled "Why the Circle Encloses the Largest Area | Explained using Hill Climbing" provides a detailed explanation of this concept.
Additionally, the video "Perimeter and Area Ratios of Similar Figures" elaborates on the relationships between the perimeters and areas of various shapes, enhancing comprehension of these mathematical principles.