Chapter 1: Introduction to Oxford's Mathematical Aptitude Test

Happy Friday! I hope your week has been productive, and now it's time to unwind with an exciting math puzzle from the University of Oxford. This question comes from the Oxford MAT, an assessment designed for prospective mathematics students. Are you ready to employ your calculus skills to tackle this challenge? Here's a hint: you don't need to compute specific values!

Pause for a moment, grab your pen and paper, and give it a try. Once you're ready, continue reading for the solutions!

The first video explores the experiences of an Oxford student, offering insights that may inspire your problem-solving journey.

Integral (a)

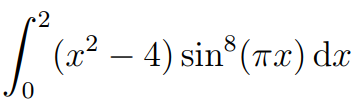
The function here is a product of (x² - 4) and sin(πx). It's crucial to note that this integral spans from x = 0 to x = 2.

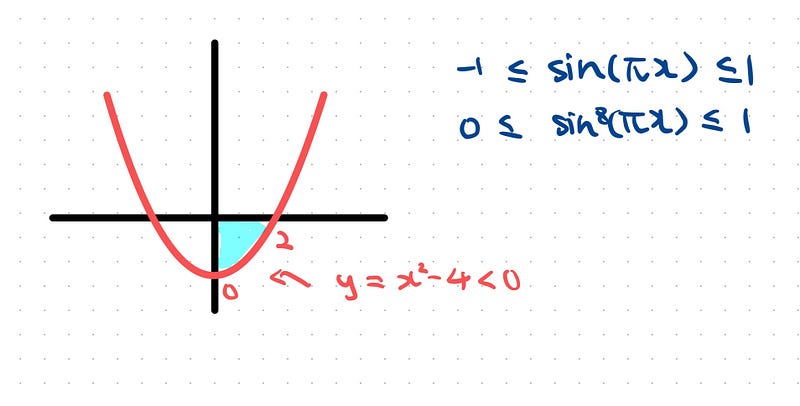
The parabola described by y = x² - 4 remains at or below zero between x = 0 and x = 2. The sine function, sin(πx), oscillates between -1 and 1, and when raised to the 8th power, it transforms the range to [0, 1]. This means we have a negative product multiplied by a positive product. Therefore, this integral will yield a negative value when evaluated from x = 0 to x = 2.

Integral (b)

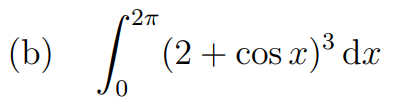
This function represents the cosine graph shifted up by 2 units. Given that the cosine function oscillates between -1 and 1, the expression 2 + cos(x) oscillates between 1 and 3, remaining always positive.

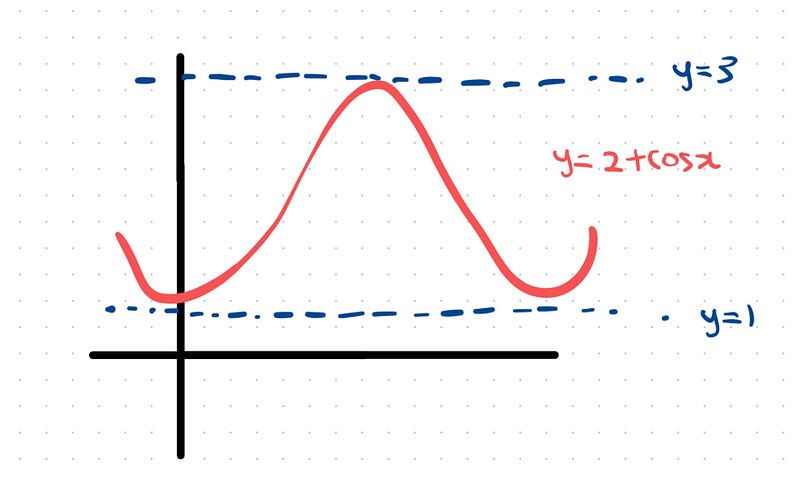
The maximum value of (2 + cos(x))³ is calculated to be 27. Consequently, we can ascertain that this integral is positive and capped at less than 54π.

Integral (c)

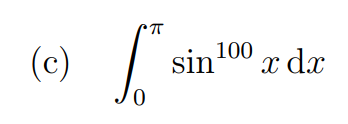
The function sin^100(x) may appear complex, but similar reasoning as before applies. The sine function's range is [-1, 1], and raising it to the 100th power ensures it remains positive, leading to a maximum value of 1. Thus, the range for this integral is [0, 1], with the minimum value being 0 and the maximum being π.

Integral (d)

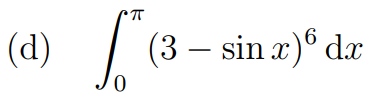
If you’ve followed along, this should be straightforward! The expression 3 - sin(x) oscillates between 2 and 4. We need to determine the lower bound, which results in a minimum value of 64π.

Integral (e)

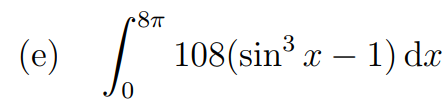
Since we established that integral (d) is at least 64π, it surpasses integrals (a), (b), and (c). Our final task is to assess whether this integral is greater than integral (d). The range for sin³(x) is [-1, 1], leading to a range of [-2, 0] for sin³(x) - 1.

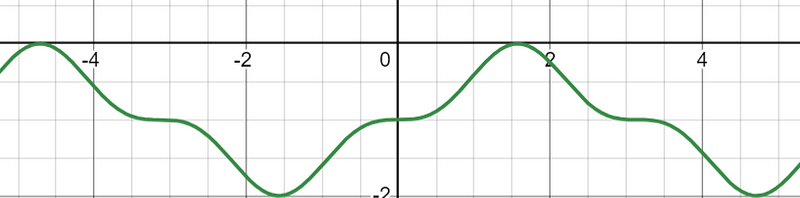
This graph reinforces that this integral will indeed yield a negative value.

Final Insights

From our evaluations, we can conclude that integral (d) is the highest, as its lower boundary exceeds that of the other integrals.

What a fascinating process! I'm eager to hear your thoughts on this challenge—please share them in the comments below.

For further exploration, check out this video on student experiences at Oxford:

This second video features street interviews, where students share their insights on gaining admission to Oxford University.

Thank you for reading! If you found this article insightful, consider giving it a clap. Your support is much appreciated!

If you feel generous, consider buying me a coffee to support my writing journey. Happy solving!