Eratosthenes and His Remarkable Measurement of Earth's Circumference
Written on
Chapter 1: Understanding the Shape of the Earth
In ancient Greece around 200 BC, scientists were already convinced that the Earth was not a flat disk but a sphere. Pythagoras considered the circle as the epitome of perfection, making it a fitting model to describe the world’s excellence. Meanwhile, Aristotle contributed to this understanding through his philosophical theories, which included the idea that all physical forms strive for a perfect state, represented by a circle.
During lunar eclipses, the Earth's shadow gradually covers the moon, revealing a spherical shape. This observation led to a logical conclusion: if the Earth casts a round shadow, it must also be spherical. This reasoning was both sound and compelling.
Eratosthenes, a prominent thinker of the time, sought to uncover the true size of the Earth.
Section 1.1: The Summer Solstice Observation
To determine the Earth's circumference, Eratosthenes could not simply measure the distance traveled around it. Instead, he focused on the summer solstice in Alexandria, where he noticed that the bottom of a well remained partially dark at noon—a black spot that was not illuminated by the sun.
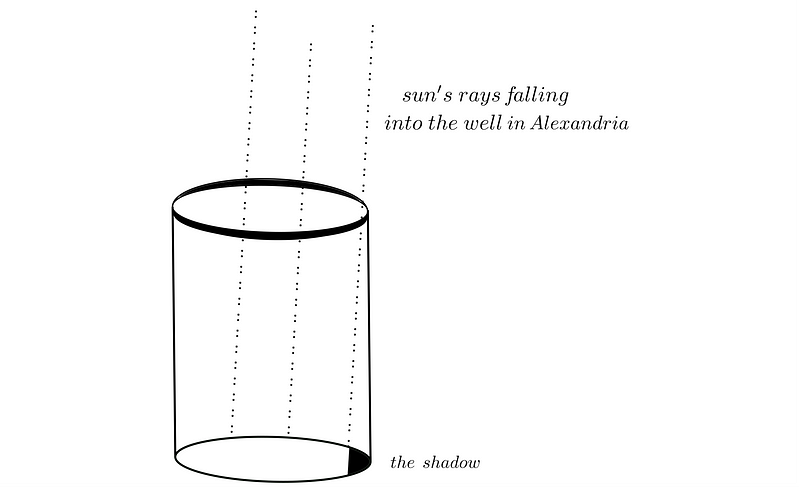
He reasoned that if the sun was directly overhead, its rays must be parallel, and therefore, they could not strike the ground perpendicularly. To find the angle of inclination, he inserted a stick into the ground and measured the angle between it and its shadow.
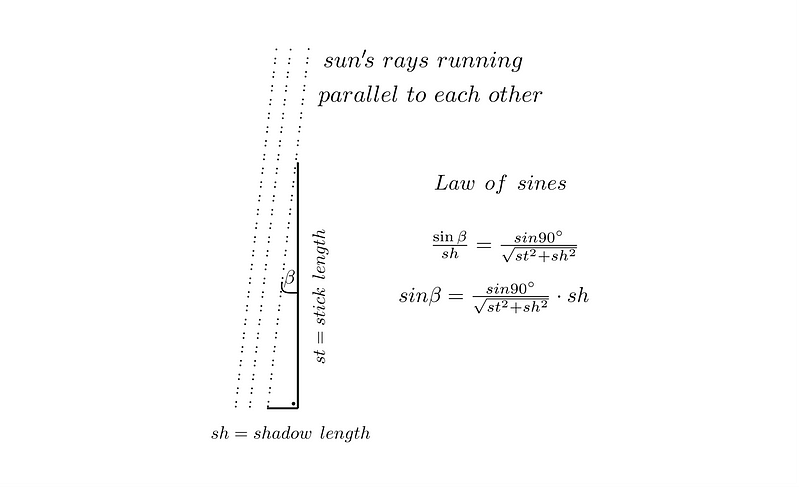
He discovered an angle of 7.12°. He then learned that in Syene, during the same solstice, the sun's rays illuminated the entire well, indicating they struck it perpendicularly. This phenomenon suggested that the Earth’s curvature could explain why sunlight hit at different angles in different locations at the same time.
Section 1.2: Calculating the Circumference
Eratosthenes realized that the difference in angle between Alexandria and Syene was 7.12°, which constituted approximately 1/50.56 of a full circle. By measuring the distance between the two cities and applying this ratio, he could estimate the Earth's circumference.
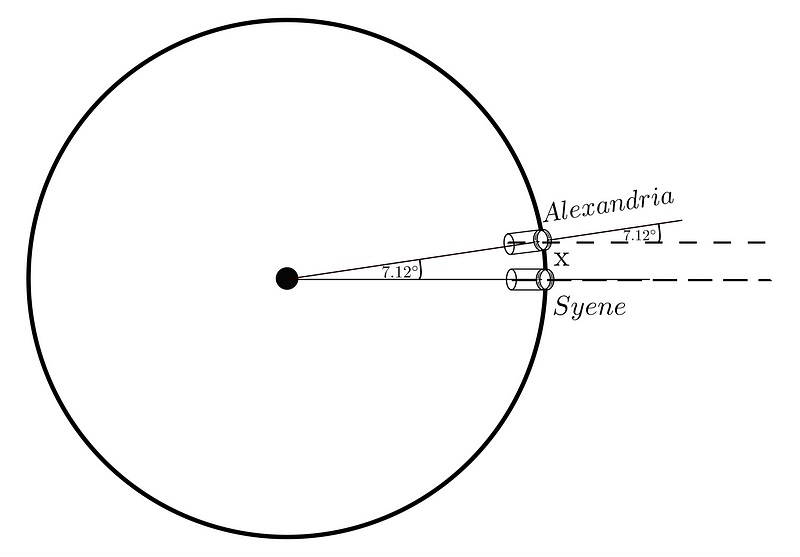
How he determined the distance remains somewhat unclear. Some suggest he relied on knowledge from caravan routes, while others believe he might have measured the distance himself. Regardless, he concluded that the distance was about 5,000 stadia, where one stadium was roughly equal to 600 Greek feet.
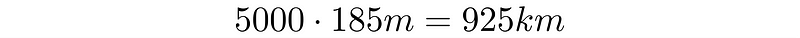
Using a conversion factor of approximately 185 meters per stadium, he calculated the circumference.
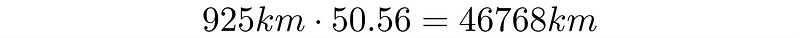
Ultimately, his estimation of the Earth's circumference was around 40,075 kilometers, which is remarkably close to the actual figure, especially considering that he assumed the Earth was perfectly spherical—a notion we now know is not entirely accurate.
Chapter 2: Eratosthenes' Legacy
This video explains how Eratosthenes calculated the Earth's circumference and explores the techniques he used to arrive at his impressive figure.
This second video delves deeper into the methods Eratosthenes employed in his groundbreaking calculation of the Earth's size.