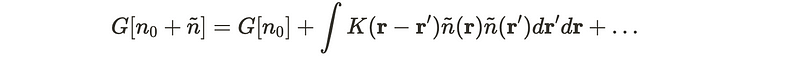Exploring Density Functional Theory: Ground State and Beyond
Written on
Chapter 1: Introduction to Density Functional Theory
In the preceding section, we aimed to establish a link between two significant physical entities. The first entity is the electron density associated with the ground state, which provides insight into the arrangement of electrons in their lowest energy configuration. The second entity concerns the external potential that influences our electron gas.
We demonstrated that knowing the external potential, denoted as v(r), enables us to derive the number density function corresponding to the ground state. The ground state operates as a functional of the external potential, as this information is sufficient to define the ground state characteristics. Furthermore, the external potential determines the Hamiltonian, which can be described through the ground state energy density.
Consequently, both kinetic and potential energy can also be expressed as functionals of the ground state energy. This leads us to formulate a term that encapsulates both kinetic and potential energy. Ultimately, we can conclude that this term is a functional of the electron density function based on our previous reasoning.
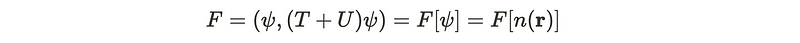
This allows us to define the total energy in relation to the ground state density.
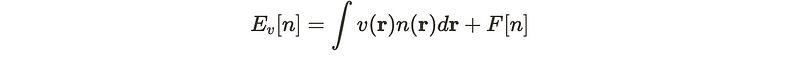
If the ground state density is accurately known, then E_v[n] will yield the correct ground state energy.
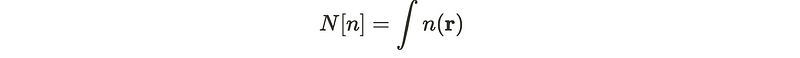
We can isolate the Coulomb interaction from the overall energy functional. This simplification makes it somewhat easier to determine the ground state.
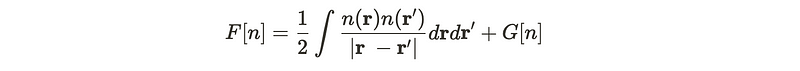
One Particle Density Matrices
In our earlier discussion, we can express the function G using one particle density matrices. A single particle density matrix can be represented as follows:
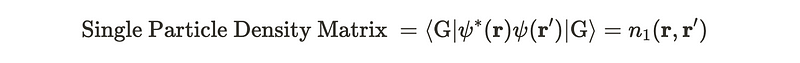
Additionally, we have a two-particle density matrix, which is quite similar and can be given by:
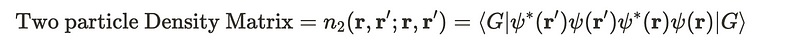
This involves two particle creation operators, which is why it is termed a two-particle density matrix. Using this concept, we can express the functional F in a slightly altered manner. Earlier, I mentioned that this term represents the sum of kinetic energy and interaction energy. The kinetic energy appears as the second term in the following sum, but I've reformulated it in terms of two distinct variables, r and r’. The interaction term is included as the third term in the sum. I have also added two terms that cancel each other out, which resemble the classical Coulomb potential between two electrons.
We also encounter an operator called the correlation function. Structuring the sum in this way allows us to consolidate the last terms.
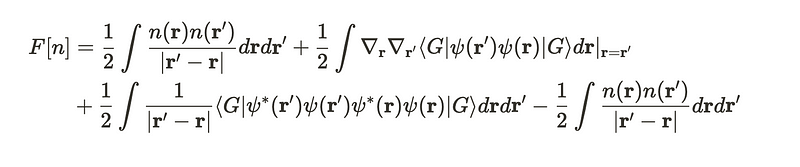
In the preceding expression, the last term resembles a correlation function, akin to those found in conventional probability theory.
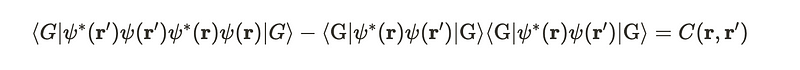
Notably, the last two terms in the sum correspond directly to this correlation function. From this, we deduce that the final expression for this function resembles a combination of a classical Coulomb force, along with the derivative of the particle density matrix and a correlation term.
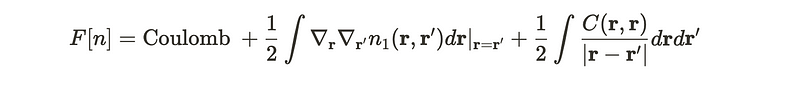
The last two terms are particularly significant. We will refer to the sum of these two terms as the functional G.
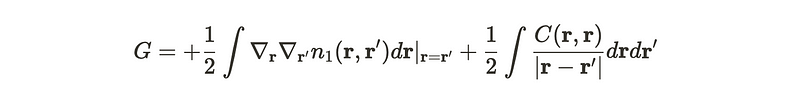
What purpose does this functional serve? One of its applications is to compute the energy of the lowest energy ground state.
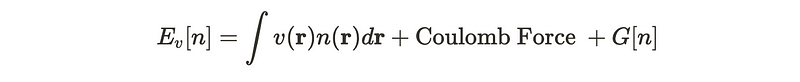
A Gas of Nearly Constant Density
In the previous segment, we undertook the task of defining several interesting functionals. Generally, we do not anticipate these computations to be straightforward. However, we can seek to simplify matters. Now, we will explore the implications of calculating the functional for simpler scenarios. What occurs when we examine a gas with approximately constant electron density, albeit with minor fluctuations?
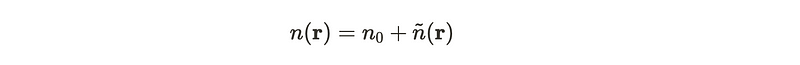
What is the G functional for a density function of this nature? We can approximate this by expanding the expression, similar to a Taylor series. In the expression below, the first term represents the functional of the constant density field, while the second term signifies the quadratic component. Notably, there is no linear term present.