Chapter 1: Introduction to Parabolas in Mathematics

For centuries, parabolas have intrigued mathematicians, including notable figures like Archimedes and Galileo. While there are many fascinating characteristics of parabolas, our focus here will be on utilizing the graph of f(x) = x² to illustrate a method for multiplying two numbers. This exploration aims to assist anyone who stumbles upon this intriguing relationship between two points on a parabola.

We will commence by developing a visual understanding of this technique, followed by a formal algebraic proof. So, let’s dive in!

To start, let’s plot the parabola described by the equation y = x².

A sensible approach to connect any two points on this parabola is to draw a line between them. By connecting various random points, we aim to discover some underlying relationship.

Now, take a moment to analyze the graph below and see if you can identify any significant relationship among the lines. (Hint: Pay attention to the y-intercepts of the lines)

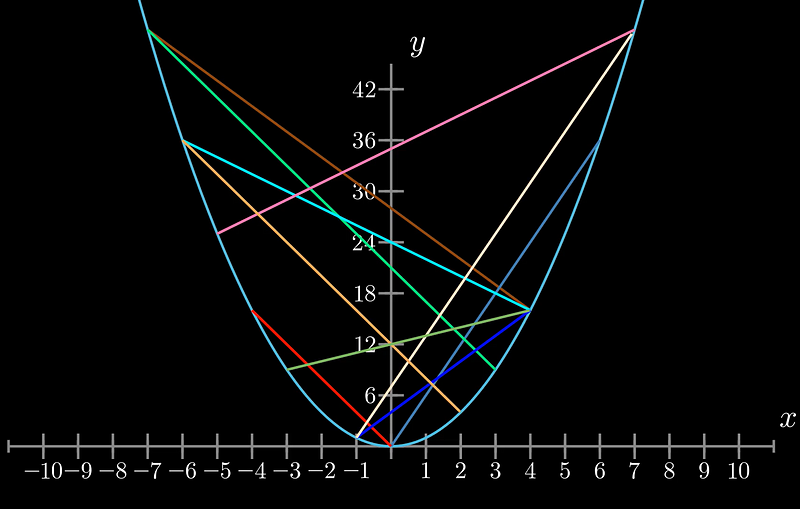
While all lines are valid, two lines in particular intersect at the y-axis at y = 12. They are noteworthy because, although they do not have the same slope and lack symmetry about the y-axis, they share a common y-intercept. To further investigate this relationship, we can simplify our graph by removing the extraneous lines.

Upon examining these two lines closely, a revealing relationship begins to emerge.

From this observation, we can hypothesize that the y-intercept of any line drawn between two points on the parabola equals the product of the x-values of the line's endpoints.

Proof

At this stage, we have gathered supporting evidence for our hypothesis, yet we still require a formal proof. With a bit of algebra, we can establish this relationship.

Chapter 2: The Quest for Prime Numbers

Once the multiplication technique is understood, you can map out all multiples and identify prime numbers by observing the gaps on the y-axis. This is referred to as a geometric sieve. To ensure precision in mathematics, we must adhere to certain guidelines:

• No line should start or end at y = 1², as every number is a multiple of 1, including primes. Consequently, if we graph the multiples of 1, a line will intersect every integer, leading to no gaps.
• Once all combinations that satisfy the condition (a)(b) = n are plotted, if no line intersects at y = n, then n is a prime number.

Concluding Thoughts

This method provides an elegant visual representation of multiplication and offers a geometric approach to identifying primes. I encourage readers to ponder how division and exponentiation might manifest on a parabola, given this newfound multiplication technique.

The first video titled "Multiplying Monkeys and Parabolic Primes" delves into the fascinating connections between parabolas and prime numbers, providing illustrative examples and engaging explanations.

The second video, "Parabolic Sieve for Prime Numbers," explores the geometric sieve method in greater detail, showcasing how it can effectively identify prime numbers using parabolic graphs.