Section 1.1: The Cyclical Nature of i

Before we delve into the solution, let’s explore the periodic characteristics of the imaginary unit.

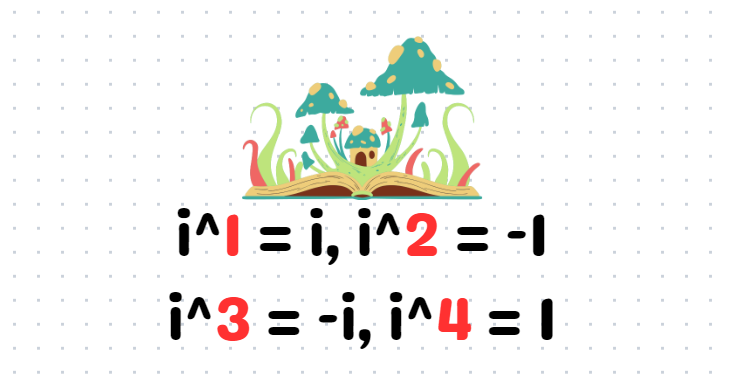
Your next challenge is to find expressions for i², i³, and i⁴. Do you notice any patterns?

Indeed, the powers of i, when expressed as positive integers, follow a repeating cycle of four: 1, -1, -i, i. This cyclical behavior provides the basis for solving this intriguing complex puzzle!

Let’s assume k is a multiple of 4. For k = 0, we find the following:

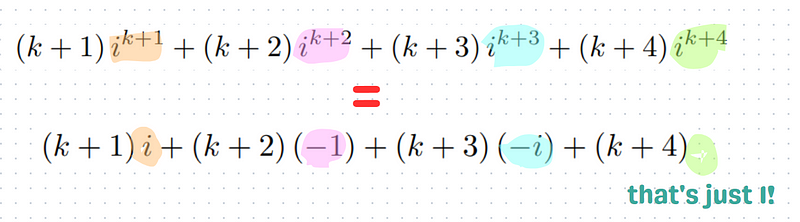
To clarify, note that if k is a multiple of 4, then i^k equals 1. Using the laws of indices, we can derive:

i^(k+1) = i^k × i¹ = i

i^(k+2) = i^k × i² = -1

i^(k+3) = i^k × i³ = -i

i^(k+4) = i^k × i⁴ = 1

At this point, the algebra should be clear.

Section 1.2: Simplifying the Expression

We can simplify our expression further:

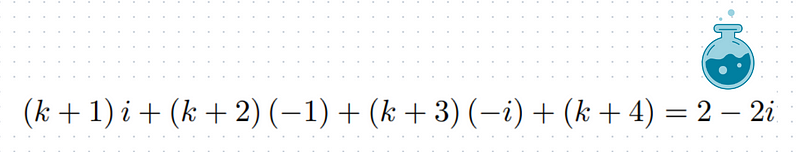
This means that for every group of four consecutive complex numbers from k+1 to k+4, the sum equals 2 - 2i.

Our ultimate goal is to ascertain how many sets of four consecutive complex numbers we require. If we select n = 4(24) = 96, we are summing from i to 96i.

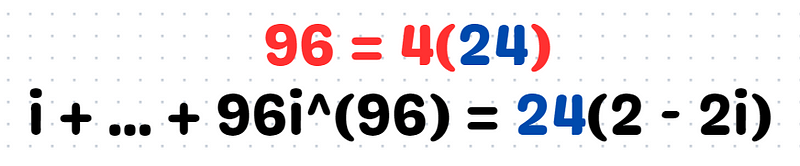
When we expand the brackets, we arrive at:

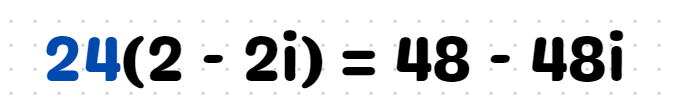
Thus, we must also include the term 97i:

From this, it is evident that 97i = 97i * i¹ = 97(1)(i) = 97i. Consequently, we find that n equals 97.

And that's our solution! How fascinating!

What was your thought process during this exercise? Please share in the comments; I’m eager to hear your insights!